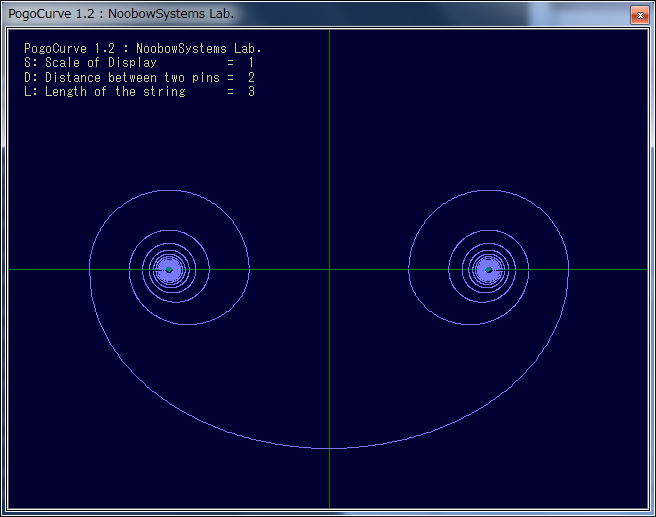
|
The Pogo Curve
Pogo's accidental discovery might lead the world of mathematics into another height. Or might not.
|
|
ここのところ毎週末、土曜の夜と日曜の夜、ポゴはウイークエンドサイエンス研究をしています。一回30分、ノート1ページ。 「パパ、昨日は天文学だったから今日はキカガクやろうよ。」 「そうだな…昨日は周期彗星が楕円軌道を持っていることをやったから、今日は楕円を描いてみよう。」 厚紙とピン2本と糸を用意して、準備完了。 「で、こうやって鉛筆で線を引いていくと、ほら、長細いマルがかけるだろ? これを楕円というんだ。 楕円は、2点からの距離の和が一定･･･こっちの線の長さとこっちの線の長さを足した長さがいつも同じになるような場所の集まりなんだ。」 「ほんとだ、面白い。やらせてやらせて。」 こんどはポゴが鉛筆を持って楕円を描き始めます。 「楕円にはこんなふうに2つの特別な点があって、これを焦点というんだ。で、彗星の楕円軌道の場合は太陽が焦点のひとつに･･･」 そしたら鉛筆を動かしていたポゴが、「あれれ?」 糸をリング状にしてピンに引っ掛けるようにしておけば、鉛筆を一周させてきれいな楕円を途切れずに描くことができます。 でもこのときは糸の端をピンに結び付けてあったので、180度を超えて鉛筆を進めると、糸がピンに引っ掛かって、 ピンを中心にした真円の描画が始まってしまうのです。 「あははっ!」といいながらポゴはそのまま鉛筆を進めて半円を描き終わり、鉛筆の先がX軸を下向きに横切ると、今度は鉛筆が長いほうの糸を引っ掛けてしまいました。 片側のピンと鉛筆の芯の間に3本の糸が通っている状態で鉛筆の先はピンの周りを半周し、 今度はまた半円を描き･･･これを繰り返して、ぐるぐる回る螺旋になってピンに近づいていき、 そのうちペン先がピンにぶつかってそれ以上描けなくなりました。 「こんなのが描けちゃった!」 「うむむ、こりゃ面白い!･･･えっと、この部分は楕円で、ここは真円で、また楕円になって、小さくなりながら無限に続いていって･･･ すごい、いったいこの曲線は何なんだ。 だいいちこの曲線の長さが無限大なのか有限なのか見当がつかない。 ポゴ、これはひょっとしたら大発見かもしれないぞ、 ポゴ曲線 の発見だ。」 「あはは。パパ、もっとポゴ曲線の研究してよ。」 ううむ、数Ⅰですでに落ちこぼれている私にとってこれは大チャレンジです。 |
 As one of the weekend science study Pogo wanted to learn something in geometry. Because in the previous night she studied about the orbits of periodic comets, I gave her a try to draw an ellipse using two pins and a string on a piece of paper. Because instead of using a looped string we tied the ends of the string to the pins, the curve drawn diverted away from an ellipse when the tip of the pencil passed the apogee of the ellipse --- the longer side of the string touched the pin and began to bend at there. The curve thus drawn was a half circle. When the tip of a pencil crossed X axis downwards, it touched the longer side of the string and started to draw a curve which is not a circle or an ellipse. The curve went into a spiral and eventually hit one of the pin. |
|
ポゴ曲線は、最初が楕円、次いで真円、また楕円･･･と思いましたが、最初の楕円を除いて2回目以降は楕円ではありません。
2つの焦点からの距離をそれぞれaとbとすると、2回目はbには糸が3回通っていて、糸の長さをLとすると
L=a+3b になっています。 どうやら曲線全体は、半分の楕円と、無限個の半円と、無限個の真円でも楕円でもない曲線から成り立っているようです。 そこで、この曲線全体を ポゴスプライン と呼び、真円でも楕円でもない曲線のひとつを ポゴ曲線 と呼ぶことにしましょう。 楕円部分と半円部分はすぐにわかりますが、いったいポゴ曲線はどうやって定義すればいいんだろう。 糸と鉛筆ではなくて、たとえばコンピュータ画面にポゴ曲線を描画するには、どうやったらいいんだろう。 ポゴスプラインは、2本のピンの間隔Dと、糸の長さLが与えられれば一意に決まります(あるいは、線対称な2つが決まります)。 DとＬの比が等しいポゴスプラインはお互いに相似です。ただしここでは、DとLの間に制約 D<L<2D を課します。 糸の長さがピンの間隔より短いと作図できませんし、糸がピン間隔の2倍以上だと「2本のピンで糸を巻き取る」部分が出てきて、ややこしくなってしまいますから。 ポゴスプラインの総延長を計算することはできるのだろうか? これは無限級数の総和として表すことができるはずだから、 数学のテキストとにらめっこを続ければ自分にもきっとできるはずです。それが無限大であっても有限値であっても。 |
 When Pogo accidentally discovered this curved line, we named it "A Pogo Curve". But soon we know that the curved line is made from some parts. Therefore we renamed it to "A Pogo Spline". Above picture shows that an Pogo Spline consists of a half ellipse, infinite numbers of half circles, and infinite number of true "Pogo curves." And later we see that the half ellipse is a special case of the Pogo Curve (at n = 1). |
|
第3研究所で、LibreOffice Drawを使って近似でもいいからポゴ曲線を描いてみようと思いましたが、
ベジエ曲線機能ではうまく描くことができませんでした。
Mathematicaなどの数学ソフトウェアを使えば簡単なのでしょうが、いまから習うのもなあ。
なにか簡単な方法で描画できないかな。 その昔はこの手の問題はたいていBASICで計算したりグラフを描いたりしてしました。 中央研究所なら Noobow9000のWindows95 でBASIC/98を使う手もありますし、2台あるPC-9801を復活させてN88BASIC(86)を使うとか、 さらにはAppleIIのApplesoft BASICもあるな。そりゃ楽しそうだ。 でも2年前に火を入れたときはAppleIIは10分かそこらでクラッシュしちゃってたから、マザーボードの点検とサービスをしてからでないと。 いずれにしろ第3研究所では無理です。 まさかグラフィック機能のないCASIO FX-702Pで計算するというのもストイックすぎるし、 VisualBASICでもいいでしょうけれど、やはり気軽にという雰囲気ではありません。 で、ちょっと探して、おお、よさそうなBASICインタプリタがある。 無料だし、ちょっと試そうとダウンロードしようとしたら、そのプログラムはすでに自分のソフトウェアライブラリに保存されてありました。 なんだ、試そうとしてダウンロードしたのにほったらかしだったんだ。 でそのことも忘れているだなんて。 というわけで、今回初めて Tiny BASIC for Windows 1.2 を使ってみます。 なお"Tiny BASIC"というと特定の処理系を指すものではなく、文字通り小さく実装されたBASIC系処理系全般を指すと思われるので、 以降本ページではTiny BASIC for Windows 1.2 のマニュアルにもある"TBasic"という表記を使います。 配布ファイルを解凍すると実行イメージ一式が出てくるので、いわゆるインストールの必要はなし。 出だしの好感度は最高です。 起動も瞬間的で、黒いイミディエイトウインドウが現れて"OK"と表示されています。 ので反射的に PRINT "Hello World" と入れてエンターキーを押したら、Hello Worldのエコーバックが得られました。 ? 2+3 と入れたら、5と表示されました。 でもどうやらプログラムは別のウインドゥに書くみたいだな。ここに
for i=1 to 10
sum=sum+i
next
print sum
と書いて「実行」メニューをクリックしたら、イミディエイトウインドゥに"55"と表示されました。
初めての起動後ここまで3分以内。
おお、指が覚えている。つぎに、必要にして十分に書かれているヘルプを読みながら、グラフィック表示の方法をトライ。 8ビットパーソナルコンピュータ時代のBASICインタプリタとWindows3.1時代のVisualBASICの雰囲気がいい感じでミックスされた構文・文法・作法は、 現場の利便最優先といった感じで、お手軽プログラミングにもってこいです。 1時間のうちにグラフ表示のための基本操作は習得できました。 さあ、道具は用意できた。 |
 In order to pursue the mystery of Pogo Spline, I used TinyBASIC for Windows Version 1.2. This BASIC interpreter runs well also on Windows7, providing functionality powerful enough to handle this type of problems. Its language is a golden mixture of good-old-days 16 bit BASIC (especially the Microsoft - NEC N88BASIC) and the flavor of VisualBASIC for the Windows 3.1. I could immediately start to write the PogoCurve program just after it was installed. |
|
すでに書いたようにポゴスプラインは、楕円(の半分)と、無限個の半円と、無限個の楕円でも真円でもない曲線から構成されています。
この楕円でも真円でもないひとつの曲線を以降ポゴ曲線と呼びましょう。
楕円と半円をコンピュータのグラフィックスに描画する方法は分かっていますから、
ポゴ曲線の計算方法がわかればポゴスプラインの全体を描くことができます。 ここでは、ピンの間隔Dと糸の長さLの関係に D < L < 2D という制約を課します。 糸の長さが最初からピンの間隔に満たなければポゴ曲線は作図できませんし、 糸の長さがピン間距離の倍よりも大きいときは「ピン2本で糸を巻き取る」部分も考えなければならないからです。 ペンを運んでいって最初に描くポゴ曲線は、右図のような三角形の頂点の集合です。 三角形の角Aと各辺の長さの関係は、余弦定理を使って  と表すことができます。 このとき三角形の辺のひとつbは、糸が3回通っています。 糸の全長をLとすると、 L = a + 3b になっています。 さらにペンを動かし続けて、2巡めのポゴ曲線では、bの辺は糸が5回通っています。 bに糸が通っている回数をnとして、糸の長さによる制約  (ただし n = 3, 5, 7, ...) があるわけですからこれをを代入して、   この式を整理すると、次のbについての二次方程式  を得ます。 ピン間距離D、糸の長さLを与えれば、0度～180度の間の任意の角度における辺の長さbは、この二次方程式を解くことによって得られます。 ここまでくれば、あとは二次方程式の根の公式を使えばいいだけです。 単純に公式に代入すれば次の式  を得ます。 なんかややこしいなあ。 もうすこし簡単に変形できるでしょうが、 計算機の準備ができているのでここは省力。 TBasicで書いたプログラム --- pogocurve.tbt と名づけました --- にポゴ曲線描画ルーチンを書き込み、 しばらくのデバッグののち、楕円と半円とポゴ曲線がきれいにつながり、ポゴスプラインがディスプレイに現れました。 TBasicは限定的ながらWindowsユーザーインターフェイス機能も持っているので、 これを使ってポゴスプラインのパラメータを簡単に変えて描画できるようにしてみました。 サンデープログラムの完成!! |
 A triangle at the Pogo Curve. |
|
1巡め、2巡め･･･とピンの周りに収束していくポゴスプラインを見ていて、
あれ、ひょっとしたら一番最初の楕円は、0巡目のポゴ曲線として表せるのかもしれない。 はたして、上述のポゴ曲線の式F.05に n = 1 を代入すると、式はbについての二次の項が消えて簡単な形になります。 なるほど、楕円はポゴ曲線の特別な場合になっているわけだ。 これはと思い、pogocurve.tbtプログラムのポゴ曲線計算ルーチンにn=1を渡してみたら･･･残念、二次方程式の根の公式の計算でゼロ除算となってしまいます。 まあ当然だな。 PogoCurveプログラムの中で楕円描画部分は別扱いのままですが、 楕円描画ルーチンでいままで使っていた楕円の公式のかわりにポゴ曲線のn=1の場合の式 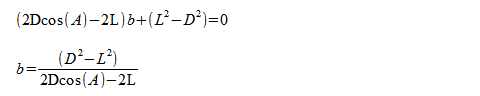 を使った座標計算に置き換えてみると、楕円公式と同じ曲線を描くことができました。 やはり楕円はポゴ曲線の特殊ケースになっているのです。 ･･･もっともこれは当然のことですね。 ポゴ曲線は、「2点からの距離の和が等しい点」という楕円の定義に条件を加えていったものなのですから、 条件を緩和していけばもとの楕円に戻るのです。 いっぽう、nをどんどん大きくしていくと、ポゴ曲線はどんどん短くなっていきますが、 その形は半円に限りなく近づいていくはずです。 |
|
いままで D<L<2D の関係を制約してきましたが、それ以上ではどうなるだろう。
たとえば 2D<L<3D ならどうなるだろう。
絵を描いてみて、2D<L<3Dの場合は同じ計算方法が使えることがわかりました。
つまり今の計算方法は D<L<3D で有効です。
右図は L=2.99D のときのポゴスプライン。 TBasicはSavePicture文があり、この1行を書き加えるだけでグラフィックス画面を簡単に画像ファイルに保存できます。 この機能を使ってPogoCurveプログラムを改造し、L=1DからL=3Dまでのポゴスプラインの形を複数の画像ファイルに書き出し、 画像ファイルをまとめてムービーにしてみました。右参照。 で、次に 3D<L<5D になると、右のピンと左のピンをそれぞれ回ることになるので、糸の長さの関係式が変わってきます。 1巡めのポゴ曲線での束縛式は
L=3a+11b L=3a+14b 次の条件は 5D<L<7D で、
L=5a+12b L=5a+17b ･･･ ポゴファクターμが 3, 5, 7, 9,･･･ にぴったりのときは、移動するペン先は焦点ぴったりを終点として終わり、 ポゴ曲線はまったく現れないことになります。 さらに、μが3や5や7よりもほんのちょっと小さいときに最大のポゴ曲線が現れます。 μが3や5や7よりもほんのちょっと大きいと、とても短いポゴ曲線が現れます。 横軸にμを、縦軸に一巡めのポゴ曲線の長さをとってグラフを描くと、2Dを周期とするノコギリ状のグラフが現れるでしょう。 でも斜めの線の傾きは一定じゃないだろうな。 ポゴファクターμが3より大きく、かつ2n+1 (nは自然数)に等しくないとき、最初の楕円のあと最初のポゴ曲線が現れるまでにさらに半円が現れます。 ポゴスプラインの総延長が無限大なのか有限値なのかまだ調べていませんが、総延長はμのなんらかの関数であることは違いなさそうです。 μが2n+1 (nは自然数)に等しければ総延長は最初の半楕円と有限個の半円の和なので、明らかに有限ですし、 それよりちょっとでもμが小さいとぐるぐるポゴ曲線と半円が永遠に続いて、μが2n+1ぴったりだったときの総延長より明らかに長いですから。 2n+1ぴったりでないμに対するポゴスプライン(これを以降 一般ポゴスプライン と呼びます)の総延長が無限だと仮定すると、 それは半円の弧長とポゴ曲線の長さでできる無限級数が発散するからです。 であれば、1巡めのポゴ曲線の長さが長かろうが短かろうが、やはり発散するはずです。 たとえばμ=3.00001でも、μ=4.99999でも、無限大のはず。 ポゴスプラインの総延長はμが2n+1ぴったりのときだけ有限値で、それ以外では無限大･･･というのはちょっと考えにくいなあ。 となると、一般ポゴスプラインの総延長はやはり有限値なんだろうか。 |
 We call the ratio L / D as a "Pogo Factor", and denotes as μ. It is the only parameter which defines the shape of a Pogo Spline. A Pogo Spline at μ = 2.99 is shown here.  Here you see how the Pogo Spline changes its shape with respect to the Pogo Factor. The current version of PogoCurve program can handle only up to μ=3. For a larger μ, it has to be modified so that it could handle the Extended Pogo Curve. [Click picture for larger video] |
|
さて、ポゴ曲線を求めるには前述の二次方程式を解くわけですが、
このとき根は二つ得られます。
そのうちの片方だけが有意なポゴ曲線を与えるのですが、
それではもうひとつの根はいったい何を意味するのだろう?
偽ポゴ曲線? 反ポゴ曲線? 虚ポゴ曲線? それとも超ポゴ曲線?
片側だけが有意であるという別の制約条件がなにかあるのだろうか? 二次方程式の2つの根のうちポゴ曲線の解として正しいのは、根の公式のプラスマイナスでマイナスをとったときだけ。 もうひとつの、プラスで計算した根を使うと、bに大きな値が得られてしまい、b側だけで糸の長さLを超えてしまいます。 ということは、線分aの長さが負になるということです。 いまD=2、L=3として最初のポゴ曲線で角A=0のときを計算すると、正しい値 b = 0.5 のほかに b = 1.25 が得られます。 1巡めのポゴ曲線ではbには3本の糸が通っていますから、 L = a + 3b の式から線分aの長さは -0.75 になります。 計算に使った余弦定理は であり、aは自乗して使われるので、式はaが負でも成立するわけです。 でも、長さが負ってどういうことなんだかやっぱり理解できません。 |
| μが1であればポゴスプラインは2本のピンをつなぐ直線に一致しますから、1以上のすべてのμについてポゴスプラインは描画できそうです。 では、μが1未満の場合はどうなるだろう。 もちろんこれは糸が2本のピン間隔より短いということなので、そもそもの作図が成り立ちません。 でも数学的にみるとどうだろう。 たとえば解析接続で複素平面に拡張するとかなんとかでμの定義域を1未満に･･･0を超えて負のμにまで･･･拡張できたりするんだろうか? あるいは、μの定義域を1以上の実数に限らず、実部が1以上の複素数を取るとしたら、ポゴスプラインっていったいどんなものになるのだろうか? |
| いままで平面上でポゴスプラインを考えてきましたが、これを3次元空間に拡張したらどうなるだろう。 2つの焦点を結ぶ直線の周りに回転するイメージかな。 でもそれは曲面が交差した複雑なものになりますね。 |
| ･･･こいつを考えるのは、すくなくとも第二種完全楕円積分が理解できてからにしよう。 |